Category: R

Here is a toy example of implementing Newton’s method in R. I found some old code that I had written a few years ago when illustrating the difference between convergence properties of various root-finding algorithms, and this example shows a couple of nice features of R.

Newtons method is an iterative root-finding algorithm where we start with an initial guess \(x_0\) and each successive guess is refined using the iterative process:

$$ x_{n+1} = x_n – \frac{f(x_n)}{f'(x_n)} $$

Here is a simple implementation of this in R:

[source lang=”R”]
newton <- function(f, tol=1E-12,x0=1,N=20) {
h <- 0.001
i <- 1; x1 <- x0
p <- numeric(N)
while (i<=N) {
df.dx <- (f(x0+h)-f(x0))/h
x1 <- (x0 – (f(x0)/df.dx))
p[i] <- x1
i <- i + 1
if (abs(x1-x0) < tol) break
x0 <- x1
}
return(p[1:(i-1)])
}
[/source]

Note a couple of things:

* The step-size for numerical differentiation is hardcoded to be 0.001. This is arbitrary and should probably be a parameter.
* The algorithm will run until either the number of steps N has been reached, or the error tolerance \(\left|x_{n+1}-x_n\right|< \epsilon\), where \(\epsilon\) is defined as the tolerance parameter tol. * The function returns a vector of the iterated x positions, which will be <= N. Here is a simple example: for instance, to find the zeros of the function $$ f(x) = x^3 + 4x^2 - 10 $$ which in R we can represent as: [source lang="R"]f <- function(x) { x^3 + 4*x^2 -10 }[/source] Let's plot the function over the range [1,2]:

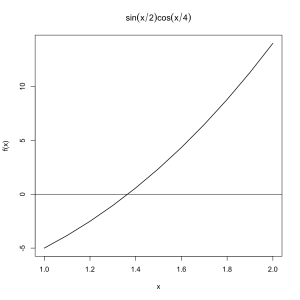
[source lang=”R”]
plot(x,f(x), type=’l’, lwd=1.5, main=expression(sin(x/2) * cos(x/4)))
abline(h=0)
[/source]

It seems obvious from the plot that the zero of f(x) in the range [1,2] is somewhere between x=1.3 and x=1.4.

This is made even more clear if we tabulate the x,y values over this range:

[source lang=”R”]
> xy <- cbind(x,f(x))
> xy
x
[1,] 1.0 -5.000
[2,] 1.1 -3.829
[3,] 1.2 -2.512
[4,] 1.3 -1.043
[5,] 1.4 0.584
[6,] 1.5 2.375
[7,] 1.6 4.336
[8,] 1.7 6.473
[9,] 1.8 8.792
[10,] 1.9 11.299
[11,] 2.0 14.000
[/source]

Using the function defined earlier, we can run the root-finding algorithm:

[source lang=”R”]
> p <- newton(f, x0=1, N=10)
> p
[1] 1.454256 1.368917 1.365238 1.365230 1.365230 1.365230 1.365230
[/source]

This returns 1.365230 as the root of f(x). Plotting the last value in the iteration:

[source lang=”R”]
> abline(v=p[length(p)])
[/source]

In the iteration loop, we use a schoolbook-style numerical derivative:

$$ \frac{dy}{dx} = \frac{f(x+\epsilon)-f(x)}{\epsilon} $$

Its also worth noting that R has some support for symbolic derivatives, so we could use a symbolic function expression. A simple example of symbolic differentiation in R (note that R works with expression instances when using symbolic differentiation):

[source lang=”R”]
> e <- expression(sin(x/2)*cos(x/4))
> dydx <- D(e, "x")
> dydx
cos(x/2) * (1/2) * cos(x/4) – sin(x/2) * (sin(x/4) * (1/4))
[/source]

In order for this to be useful, obviously we need to be able to evaluate the calculated derivative. We can do this using eval:

[source lang=”R”]
> z <- seq(-1,1,.1)
> eval(dydx, list(x=z))
[1] 0.3954974 0.4146144 0.4320092 0.4475873 0.4612640 0.4729651 0.4826267
[8] 0.4901964 0.4956329 0.4989067 0.5000000 0.4989067 0.4956329 0.4901964
[15] 0.4826267 0.4729651 0.4612640 0.4475873 0.4320092 0.4146144 0.3954974
[/source]

Note that we can bind the x parameter in the expression when calling eval().

Last week I gave a presentation to the Melbourne R User Group on Building R Packages. The talk covered a simple package example, and an example of interfacing R with native code. The slides are here:

RPackages.pdf.

The R community in Melbourne (and Australia in general) is exploding, and it was great to see so many people from different backgrounds there. Looking forward to the next event!

When debugging R interactively, one hurdle to navigate is unwrapping SEXP objects to get at the inner data. Gdb has some useful macro functionality that allows you to wrap useful command sequences in reusable chunks. I recently put together the following macro that attempts to extract and print some useful info from a SEXP object.

It can be used as follows. For instance, given a SEXP called “e”:

(gdb) dumpsxp e
Type: LANGSXP (6)
Function:Type: SYMSXP (1)
"< -" Args:Type: LISTSXP (2) (SYMSXP,LISTSXP)

We can see that e is a LANGSXP, and the operator is “< -". Functions have different components - here we can see the function representation (the SYMSXP) and the function arguments (the LISTSXP).

Some knowledge of LANGSXP structure is useful here. For instance, if we know that for a LANGSXP that CAR(x) gives us the function and CDR(x) gives us the arguments, we can view the components individually.

To see the first component:

(gdb) dumpsxp CAR(e)
Type: SYMSXP (1)
"< -"

The arguments are given by the CDR of e. We can then crack open the list and view the function arguments, recursively looking through the pairlist until we get to the end:

(gdb) dumpsxp CDR(e)
Type: LISTSXP (2)
(SYMSXP,LISTSXP)
(gdb) dumpsxp CADR(e)
Type: SYMSXP (1)
"x"
(gdb) dumpsxp CADDR(e)
Type: LANGSXP (6)
Function:Type: SYMSXP (1)
"sin"
Args:Type: LISTSXP (2)
(REALSXP,NILSXP)
(gdb) dumpsxp CADDDR(e)
Type: NILSXP (0)

The NILSXP tells us that we’ve got to the end of the list.

The GDB macro is below. Put it in your .gdbinit to automatically load it when gdb starts up.

[sourcecode language=”c”]
define dumpsxp
if $arg0==0
printf "uninitialized variable\n"
return
end

set $sexptype=TYPEOF($arg0)

# Typename
printf "Type: %s (%d)\n", typename($arg0), $sexptype

# SYMSXP
if $sexptype==1
# CHAR(PRINTNAME(x))
print_char PRINTNAME($arg0)
end

# LISTSXP
if $sexptype==2
printf "(%s,%s)\n", typename(CAR($arg0)), typename(CDR($arg0))
end

# CLOSXP
if $sexptype==3
dumpsxp BODY($arg0)
end

# PROMSXP
# Promises contain pointers to value, expr and env
# tmp = eval(tmp, rho);
if $sexptype==5
printf "Promise under evaluation: %d\n", PRSEEN($arg0)
printf "Expression: "
dumpsxp ($arg0)->u.promsxp.expr
# Expression: (CAR(chain))->u.promsxp.expr
end

# LANGSXP
if $sexptype==6
printf "Function:"
dumpsxp CAR($arg0)
printf "Args:"
dumpsxp CDR($arg0)
end

# SPECIALSXP
if $sexptype==7
printf "Special function: %s\n", R_FunTab[($arg0)->u.primsxp.offset].name
end

# BUILTINSXP
if $sexptype==8
printf "Function: %s\n", R_FunTab[($arg0)->u.primsxp.offset].name
end

# CHARSXP
if $sexptype==9
printf "length=%d\n", ((VECTOR_SEXPREC)(*$arg0))->vecsxp.length
#print_veclen $arg0
print_char $arg0
end

# LGLSXP
if $sexptype==10
set $lgl=*LOGICAL($arg0)
if $lgl > 0
printf "TRUE\n"
end
if $lgl == 0
printf "FALSE\n"
end
end

# INTSXP
if $sexptype==13
printf "%d\n", *(INTEGER($arg0))
end

# REALSXP
if $sexptype==14
print_veclen $arg0
print_double $arg0
end

# STRSXP
if $sexptype==16
print_veclen $arg0
set $i=LENGTH($arg0)
set $count=0
while ($count < $i)
printf "Element #%d:\n", $count
dumpsxp STRING_ELT($arg0,$count)
set $count = $count + 1
end
end

# VECSXP
if $sexptype==19
print_veclen $arg0
end

# RAWSXP
if $sexptype==24
print_veclen $arg0
end

end

define print_veclen
printf "Vector length=%d\n", LENGTH($arg0)
end

define print_char
# this may be a bit dodgy, as I am not using the aligned union
printf "\"%s\"\n", (const char*)((VECTOR_SEXPREC *) ($arg0)+1)
end

define print_double
printf "%g\n", (double*)((VECTOR_SEXPREC *) ($arg0)+1)
end
[/sourcecode]